



Types (semi-) numériques
Syntaxe
Types numériques
Types structurés
Expressions
Évaluation
Procédures
Les correspondances ne sont pas parfaites et il vaut mieux garder à l'esprit quelques différences.
Vue d'ensemble
Le tableau ci-dessous récapitule ce qui peut être appelé nombre en Maple [1].| données | exemple | whattype | type( ? , ...) | ||
| entiers | 2 | integer | rational | numeric | realcons |
| fractions | 3/4 | fraction | |||
| décimaux | 3.1416 | float | |||
| expressions | exp(2) | function | |||
| Pi + ln(2) | ' + ', ' * ', ' ^ ' | ||||
| complexes | 2+3*I, sqrt(-1) | complex { ( ... ) } | |||
Maple associe à chaque donnée un type de base. C'est ce qu'on obtient comme réponse à whattype(donnée).
Mais on peut aussi tester une donnée par rapport à un type dérivé [2] par type(donnée , type_dérivé) (qui retourne true ou false).

Entiers
Le type Maple de base integer correspond à l'ensemble des entiers relatifs (Z) [3].Citons quelques fonctions utiles portant sur les entiers :
- length(n) donne le nombre de chiffres de l'entier n.
- le quotient de la division euclidienne de a par b se note iquo(a,b) ;
- le reste de la division euclidienne de a par b se note irem(x,y) [4] ;
- la factorielle de l'entier n se note n! [5] ;
- la parité (resp. l'imparité) de l'entier n peut être testée avec type(n,even) (resp. type(n,odd)).

Fractions
Il s'agit des rationnels non entiers, car le type de base d'une donnée doit être unique et une fraction telle que 6/3 est automatiquement simplifiée à 2 [6].Ceci explique la nécessité du type dérivé rational.
On obtient le numérateur d'une fraction avec numer(r) ou la syntaxe plus générale [6] op(1,r).
On obtient son dénominateur avec denom(r) ou op(2,r).

Décimaux
Le type float correspond assez bien aux nombre décimaux mathématiques (ensemble D). Toutefois, on se gardera de confondre 2 (qui n'est pas un float) avec 2.0 (qui en est un).Typiquement, un float est le résultat d'une approximation numérique (evalf).
Un tel décimal d s'écrit de manière unique (-)a.10b avec a, b entiers et b maximal.
a est la mantisse de d qui s'obtient avec op(1,d) ;
a est la mantisse de d qui s'obtient avec op(2,d) .

Maple conserve, pour des raisons de compatibilité, la notation désuète Float(a,b) (correspondant à a.10b).

Tests de type
Dans les procédures où l'on a besoin de savoir à quel type de donnée on a affaire, l'instruction type(...) est utile :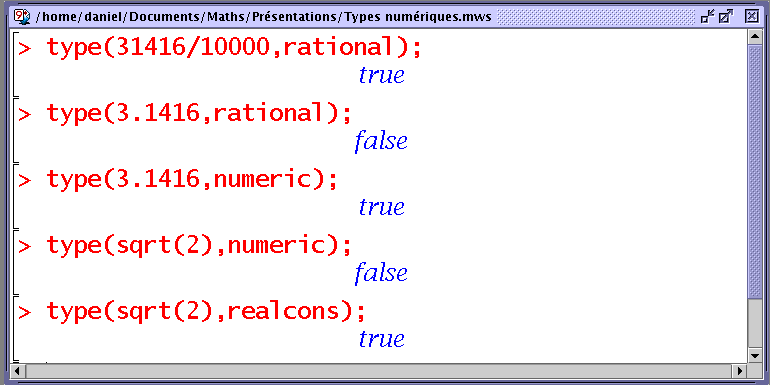

Expressions algébriques
Le type dérivé realcons englobe tout ce que Maple est capable d'approximer numériquement.| expression | whattype( ... ) |
| sqrt(2) | ' ^ ' |
| Pi + ln(2) | ' + ' |
| exp(-1) | function |
| Pi | string |
| type( ... , realcons) | true |
Dans ce cas, le résultat de le commande whattype est parfois explicite, parfois surprenant. On se reportera à la section "Expressions" pour plus de détails.
Attention ! Les données de ce type ne réagissent pas à la relation d'ordre. Il faut les approximer avec evalf avant de pouvoir les faire figurer dans des tests.


Complexes
Le type complex n'est pas un type de base, mais un type dérivé.| complexe | whattype( ... ) |
| sqrt(-1) | ' ^ ' |
| 3 + 4 * I | ' + ' |
| exp(2 * I * Pi / 3) | function |
| type( ... , complex) | true |
Les principales fonctions que l'on peut avoir à calculer en un complexe z sont :
- la partie réelle : Re(z) ou op(1,z) ;
- la partie imaginaire : Im(z) ou op(2,z) ;
- le module : abs(z) ;
- l'argument principal (dans ]- π, π]) : argument(z).

Enfin, on peut tester avec complex(sous_type) si un complexe donné présente des parties réelle et imaginaire d'un type particulier.
Là encore, on se rappellera que Maple n'effectue pas automatiquement toutes les réductions :


Notes
[1] D'une manière générale, tout ce que Maple peut approximer (avec evalf).
[2] Un type dérivé n'est jamais le résultat de la commande whattype.
[3] Maple n'implémente pas la notion d'entier naturel. On peut la tester en vérifiant le type integer et le signe.
[4] Maple ignore les notations div et mod, pourtant classiques.
[5] Cette disposition constitue ainsi une dérogation à la syntaxe classique des fonctions en Maple.
[6] Voir la section "Expressions".