



Expressions et fonctions
Syntaxe
Types numériques
Types structurés
Expressions
Expressions
Fonctions
Évaluation
Procédures
Expressions
Celles-ci doivent être représentées en interne de façon unique et non ambiguë, p. ex. afin de pouvoir juger de leur égalité.À cet effet, Maple doit effectuer automatiquement certains regroupements.
Substitutions automatiques
Voici quelques remplacements que Maple effectue systématiquement [1].| expression | substitution | commentaire |
| x + x | 2x | |
| ax + bx | (a+b)x | si a, b affectées |
| xx | x2 | |
| xaxb | x(a+b) | si a, b affectées |
| sin(π/6) | 1/2 | valeurs particulières |
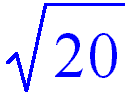 |  |
Ordre de calcul
Maple respecte généralement les conventions algébriques usuelles. On aura donc, du plus au moins prioritaire :- les fonctions unaires (exp, sin, ...) ;
- les exponentiations ^ ;
- les multiplications * (et les divisions) ;
- les additions + (et les soustractions) ;
- les booléens (=, <, ...).
À niveau de priorité égal, les calculs sont faits de gauche à droite.
Une exception notable est a^b^c, qui déclenche une erreur [3].
Le type d'une expression est celui de son opérateur de plus bas niveau
.

Conventions d'affichage
Parfois la représentation interne d'une expression n'est pas celle que Maple affiche :| affichage | représentation interne |
| x - y | x + (-1) * y |
| x / y | x * y ^ (-1) |
 | x ^ (1/2) |
Représentation arborescente...
Considérons l'expression cos(a + b) = cos(a) cos(b) – sin(a) sin(b).Nous disons que Maple la représente sous la forme d'un arbre :

Sa syntaxe générale est :
| op( indice , expression ) ; |
Si l'on extrait ses opérandes successifs...

... on se rend compte de deux choses :
- Les opérandes sont bien organisés en une arborescence descendante comme dans le schéma ci-dessus. (Ainsi, "– sin(a) sin(b)" est bien le deuxième opérande du deuxième opérande de expr.) ;
- Le "-1" est le premier opérande de "– sin(a) sin(b)", confirmant les conventions d'affichage évoquées plus haut. (Il n'y a pas de "différence" dont "sin(a) sin(b)" serait le deuxième opérande.)

Substitution
L'instruction subs permet d'effectuer un remplacement dans une expression, selon la syntaxe :| subs( motif = remplacement , expression ) ; |
Attention, subs n'agit que sur les opérandes de l'expression (résultats de op).
Pour un examen plus détaillé (et plus mathématique) de l'expression, on pourra utiliser algsubs.

Dans l'exemple ci-dessus, "x+y" n'est effectivement présent qu'une fois dans la représentation de l'expression (x+y)/(x+y+z) [4].
Seul algsubs peut détecter le "x+y" dans "x+y+z".
Plus de détails sur subs à la section "Évaluation".
Fonctions
Dans tout système de calcul formel, la différence entre fonction et expression est cruciale.- une expression est un objet algébrique inerte ;
- une fonction prend un ou plusieurs arguments et produit un résultat.

La commande fondamentale unapply fonctionne ainsi :
| unapply( expression , var1 { var2 , ... , varN } ) ; |
Par exemple :
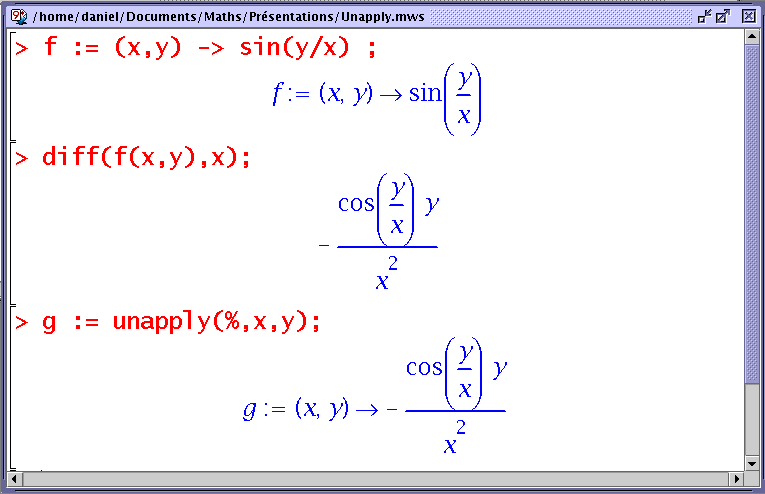
Attention, g := x - > %, bien que tentant, n'aurait pas marché. En effet, dès que le symbole "- >" apparaît, il initie la définition d'une fonction (g). Dès lors, le caractère "%" désigne le dernier résultat calculé dans le cours de la définition de g. Il ne "sort" pas de cette dernière, et ne peut donc convenir pour faire référence à un résultat extérieur à g.

Opérations sur les fonctions
Maple permet d'opérer directement sur les fonctions. Résumons les correspondances avec la notation mathématique :| mathématiquement | traduction Maple |
| f + g, f * g | f + g, f * g |
| f o g (composition) | f @ g |
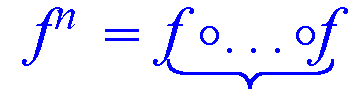 n fois "f" | f @@ g [5] |
Maple permet enfin d'utiliser des fonctions "anonymes" : (x - > 1/(1 + x^2)) (1) est correct. Cela peut servir à l'occasion, pour une fonction utilisée seulement ponctuellement.

Fonctions d'ordre supérieur
Maple est assez pauvre en cette catégorie de "fonctions sur les fonctions". Citons- map, qui applique une fonction à tous les opérandes d'une expression ;
- zip, qui s'applique à une fonction de n variables et n listes, et "enfile" la fonction à chaque ième terme des n listes ;
- select et remove, qui filtrent une liste selon qu'un critère (booléen) est satisfait ou non.

(isprime(n) est true ou false selon la primalité de l'entier n.)

Notes
[1] Il est pratiquement impossible d'empêcher Maple d'effectuer ces regroupements.
[2] Cette disposition est indispensable pour pouvoir mettre en place des (in)équations.
[3] Mathématiquement, cela aurait un sens (a^(b^c)) contraire à la convention "de gauche à droite" de Maple.
[4] En effet, l'opérande au dénominateur est x+y+z.
[5] Noter l'analogie avec la notation x ** n -- pour itérer la multiplication.