
TEX et maths
Introduction
Caractères
Maths
Le mode mathématique
Les lettres grecques
Les opérateurs
Les relations
Les flèches
Les noms de fonctions
Les fractions et les radicaux
Les symboles divers
Un exemple
Fontes
Tables
Structure
Paragraphes
Espaces
Le mode mathématique
TEX est particulièrement à l'aise pour produire des notations mathématiques, son but principal. Nul besoin d'entrer dans un quelconque "éditeur d'équations", il suffit de déclarer à TEX qu'on est en train de coder des mathématiques.
Le mode mathématique de TEX est délimité par le caractère $.
Mathématiques en ligne et centrées
Toute expression mathématique est encadrée par des $. Mais lorsqu'une formule doit être mise en évidence, seule sur une ligne (éventuellement repérée par un n°), et séparée du texte par un peu d'espace, on l'entourera de $$. Observons la différence :
math\'ematiques en ligne : $x^n+y^n=z^n$ et centr\'ees : $$x^n+y^n=z^n$$
donnera
mathématiques en ligne : xn + yn = zn et centrées :
xn + yn = zn
En mode centré, les numérateurs et dénominateurs des fractions ne sont pas réduits (sauf fractions imbriquées). Les indices des sommations ou autres opérateurs figurent au-dessus ou au-dessous de ceux-ci, plutôt qu'à leur droite (sauf pour les intégrales dont les bornes figurent toujours à droite). Les opérateurs eux-mêmes sont dessinés plus gros.
Il faut trouver le bon compromis entre la lisibilité des formules (qui est meilleure si on les centre) et de l'ensemble du document (qui deviendrait vite décousu si trop de formules étaient centrées).
Différences entre les mathématiques et le texte
TEX utilise automatiquement une police de caractères italique pour les mathématiques. Cela améliore leur lisibilité et les fait ressortir du texte.
En mode mathématique, TEX gère lui-même l'espace entre les caractères. Inutile de rajouter des espaces dans $x+y$, ils seront ignorés. Il en est de même des passages à la ligne. TEX protestera à l'occasion lorsqu'une formule est trop complexe pour être coupée harmonieusement.
Les accents ne sont plus disponibles en mode mathématique. (En fait, certains le demeurent, mais doivent être codés autrement).
Par contre, on dispose dans ce mode, outre les symboles mathématiques, de fontes particulières qui ne sont pas accessibles en dehors : majuscules calligraphiques, style fraktur (à ne pas confondre avec le style gothique), etc. (voir plus loin).
Les lettres grecques
Comment se passer de l'alphabet grec ? En mode mathématique (entre $)
| pour obtenir | on codera |
| α | \alpha |
| : : |
: : |
| ω |
\omega |
avec juste les cas particuliers suivants : \epsilon donne ϵ ; \phi donne ϕ. Pour obtenir ε et φ on codera respectivement \varepsilon et \varphi.
Les majuscules s'obtiennent en faisant débuter le nom de la lettre grecque par une majuscule (ex. \Gamma), mais les majuscules qui sont identiques à celles de notre alphabet ne nécessitent bien sûr aucun codage particulier. On écrira donc simplement A et non \Alpha, qui donnerait une erreur : pas de zèle !
D. Knuth est très à cheval sur la "belle" forme des lettres grecques !
Les opérateurs
Les opérateurs binaires standard
Nous nous contenterons des plus courants :
| symbole | codage | symbole | codage |
| + | + | ∩ | \cap |
| - | - | ∪ |
\cup |
| × |
\times | ∧ | \wedge |
| ⋅ |
\cdot | ∨ |
\vee |
| * | \ast ou * | ⊕ |
\oplus |
| ÷ |
\div | \ | \setminus |
| ∘ |
\circ | ± |
\pm |
Les "grands" opérateurs
Ceux-ci s'agrandissent automatiquement en mode centré, et leurs indices se placent alors au-dessus et en-dessous (sauf pour les intégrales).
| symbole | codage | symbole | codage |
| ∑, ∑ | \sum | ⋂, ⋂ | \bigcap |
| ∏, ∏ | \prod | ⋃, ⋃ | \bigcup |
| ∫, ∫ | \int | ⋀, ⋀ | \bigwedge |
| ⊕, ⊕ | \bigoplus | ⋁, ⋁ | \bigvee |
Les relations
Là encore, juste un petit échantillon :
| symbole | codage | symbole | codage |
| < | < | ⊃ | \supset |
| > | > | ⊇ |
\supseteq |
| ≤ | \leq | ≡ |
\equiv |
| ≥ |
\geq | ≅ |
\cong |
| ∈ |
\in | ≃ |
\approx |
| ⊂ |
\subset | ⊥ |
\perp |
| ⊆ |
\subseteq | ∝ |
\propto |
Les relations niées
Pour obtenir la négation d'une relation, la règle générale est de faire précéder son codage de \not. Par exemple : \not = donne ≠, \not \subset donne ⊄. Une exception : ∉ se code directement \notin (\not \in est possible mais donne un résultat moins esthétique).
\not permet de manière générale de "nier" n'importe quel caractère, et pas seulement les relations.
Les flèches
Les codes des flèches répondent à une syntaxe générale :
| \(long)(direction)arrow |
où
- direction peut valoir left, right, up, down selon la direction de la flèche (leftright ou updown si elle pointe des deux côtés) ainsi que ne (nord-est), se, nw, sw.
- long est rajouté si bien sûr on veut une flèche plus longue.
- le nom de la flèche commencé par une majuscule donnera une flèche double.
Par exemple :
| pour obtenir | on codera |
| ↑ |
\uparrow |
| ↔ |
\leftrightarrow |
| ⇓ |
\Downarrow |
etc. Notons quand même le codage $\mapsto$ pour obtenir ce type de flèche très utile : ↦.
Les noms de fonctions
En bonne typographie, on n'écrit pas sin(x) mais sin(x). Les noms des fonctions doivent être en lettres droites, toujours dans le souci de les mettre en évidence. Mais nous avons vu que TEX mettait les mathématiques en italiques. Par conséquent, si l'on codait $sin(x)$ on obtiendrait sin(x).
La solution n'est pas, comme on pourrait le croire, de sortir du mode mathématique ($y=$sin$(x)$). C'est malcommode, et l'espace serait mal géré (le "sin" serait trop près du texte qui le précède et qui le suit).
TEX dispose de commandes correspondant aux noms des principales fonctions : il suffit d'écrire $\sin(x)$, sans oublier l'espace après le nom de fonction si l'on écrit simplement $sin x$.
TEX connaît les noms des fonctions suivantes :
| \arccos | \cosh | \det | \ker | \log | \sin |
| \arcsin | \cot | \dim | \lim | \max | \sinh |
| \arctan | \coth | \exp | \liminf | \min | \sup |
| \arg | \csc | \gcd | \limsup | \Pr | \tan |
| \cos | \deg | \inf | \ln | \sec | \tanh |
... mais pour ceux qu'il ne connaît pas ? Pou arctan(x) p. ex., il ne faudrait pas coder $\arc\tan(x)$ (qui donnerait arc tan(x)). Il faut utiliser le langage de macros de TEX pour définir ce qui nous manque :
\def\arctan{\mathop{\rm arctan}\nolimits}
fera le travail. Dans cette construction on distingue {\rm arctan} qui force les caractères romans. \def et \mathop seront expliqués plus loin. Quant à \nolimits, il garantit que les exposants et indices éventuels seront toujours à droite du nom de la fonction, même en mode centré.
On procèdera ainsi, par exemple, pour définir les fonctions hyperboliques "à la française" ch, sh, th, argch, argsh, et argth.
Les fractions et les radicaux
Fractions
Évidemment, les fractions avec trait oblique ne posent aucun problème ($a/b$).
Pour définir une fraction avec trait horizontal, on utilisera la construction suivante :
| {numérateur \over dénominateur} |
ou sa contrepartie LATEX [1] :
| \frac{numérateur}{dénominateur} |
Si la fraction est centrée (entre $$), numérateur et dénominateur auront leurs tailles normales. Si par contre elle est en ligne (entre $), numérateur et dénominateur seront réduits. Mais cette réduction se produira même en mode centré pour des numérateurs et dénominateurs imbriqués. On peut contrecarrer ce phénomène en utilisant la commande \displaystyle.
Un exemple s'impose.
En mode centré, le codage
$$a_0+{1 \over a_1+{1 \over a_2+{1 \over a_3}}}$$
donnera
tandis que
$$a_0+{1 \over\displaystyle a_1+
{1 \over\displaystyle a_2+
{1 \over\displaystyle a_3}}}$$
donnera, lui :
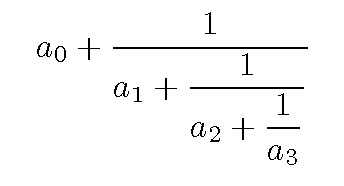
Notons la commande inverse de \displaystyle, \texstyle, qui force TEX à faire de "petites fractions" même en mode centré.
Radicaux
Une racine carrée (sans exposant) se code simplement \sqrt : $\sqrt 2$.
En ce qui concerne les radicaux imbriqués, la différence entre les modes en ligne et centré tient à l'espacement entre les barres des racines carrées successives.
Exemple en mode en ligne :
$\sqrt{a_0+\sqrt{\a_1+\sqrt{a_2+\sqrt a_3}}}$
Le même en mode centré :
$$\sqrt{a_0+\sqrt{\a_1+\sqrt{a_2+\sqrt a_3}}}$$
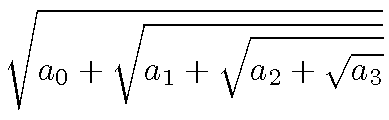
Pour des racines cubiques, n-ièmes... on utilisera la construction TEX
| $\root exposant \of radicande$ |
ou la syntaxe LATEX [1] :
| $\sqrt[exposant]{radicande}$ |
Par exemple :
$\f_n(x)=\root n \of{1+x^n}$
donnera
Les symboles divers
Pour finir, un pot pourri de symboles variés plus ou moins fréquemment utilisés :
| symbole | codage | symbole | codage |
| \ | \backslash | ∞ | \infty |
| ℵ | \aleph | ∅ |
\emptyset |
| ı |
\imath | ∇ | \nabla |
| ȷ |
\jmath | ∀ |
\forall |
| ℓ |
\ell | ∃ |
\exists |
| ℜ | \Re | ¬ |
\neg |
| ℑ |
\Im | ∠ |
\angle |
| ∂ | \partial | △ |
\triangle |
Un exemple
Pour obtenir le résultat suivant :
on coderait ainsi :
Si $f:\left[ a,b\right] \rightarrow\mathbb{R}$ est continue par morceaux sur $\left[ a,b\right] $ alors on a :%
$$
\lim_{n\rightarrow\infty}\frac{b-a}{n}\sum_{k=0}^{n}f\left( a+k\frac{b-a}%
{n}\right) =\int_{a}^{b}f\left( t\right) dt
$$
(certaines notations n'ont pas encore été introduites ; voir les sections suivantes)
Note
[1] LATEX, ou certaines de ses extensions, redéfinit certaines commandes de TEX. Mais il continue de "digérer" les commandes standard, qui produisent simplement un message d'avertissement à la compilation.



