



Les hyperensembles
Courbes & surfaces
Ensembles, nombres & graphes
En théorie "normale" des ensembles, l'axiome de fondation est là pour empêcher la constitution de "chaînes infinies d'appartenance" du type
x0 ∊ x1 ∊ x2 ∊ ... ∊ xn ∊ xn+1 ∊ ...
Cela revient à dire que le niveau d'imbrication des accolades doit être fini. Par exemple, il ne peut exister d'ensemble x tel que
x ∊ x
(prendre xn = x pour tout n).
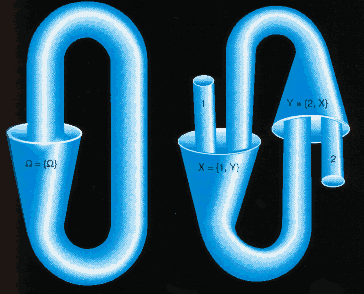
L'axiome d'antifondation d'Aczel dit tout le contraire. Selon lui, à peu près toute "équation ensembliste" admet une solution unique. Par exemple, x = {x}, ou (x = {1,y} et y = {2,x}). Cet axiome est contradictoire avec l'axiome de fondation. Les ensembles obtenus grâce à lui sont plus nombreux que les ensembles "classiques". On les appelle hyperensembles.
Mais à quoi peut bien ressembler un ensemble Ω tel que Ω = {Ω} ? On ouvre une boîte et on y trouve une boîte identique, qui contient à son tour la même boîte et ainsi de suite... Pour Y. Moschovakis, c'est le "cadeau éternellement décevant" (ultimately disappointing gift).
[Pour la Science n° 195 - 01/94]