



Le paradoxe de Hausdorff - Banach - Tarski.
Sémantique
Logique
Infini
Mesure
Probas
Nombres
Physique
Un simple schéma suffit pour comprendre ce que sont deux ensembles équidécomposables :
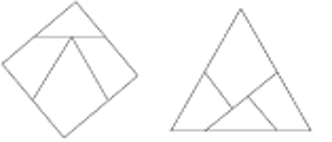
A et B sont équidécomposables s'il existe un entier n, des parties disjointes A1, ..., An de A (avec ⋃i=1nAi = A ) et B1, ..., Bn de B (avec ⋃i=1nBi = B) et des isométries g1, ..., gn avec g(Ai) = Bi (i=1, ..., n). Le carré C et le triangle équilatéral T ci-dessus sont donc équidécomposables, avec n=4. Il est alors évident qu'ils ont la même mesure (la même aire, en l'occurrence) -- puisque celle-ci est conservée par les isométries.
En 1914 fut pourtant énoncée la propriété suivante :
Théorème : Une boule de R3 de rayon 1 est équidécomposable à deux boules de R3 de rayon 1.
n valait 6 dans la démonstration initiale, ramené à 5 par la suite.Ce résultat choque l'intuition ("mais alors, une boule a le même volume que deux boules !..."). Sa généralisation complète n'est pas moins étonnante :
Théorème : Soient deux domaines A et B de R3, bornés, d'intérieurs non vides (càd, contenant une boule ouverte de rayon > 0). Alors :A et B sont équidécomposables.
On a l'impression de s'entendre affirmer que toutes les parties de R3 ont le même volume... Un lingot d'or équidécomposable à deux, trois lingots d'or... prodige ! En fait, le théorème est (bien sûr) rigoureusement inattaquable. Ce qui n'est pas le cas de ses prétendues conséquences. En fait, les parties qui interviennent dans les décompositions sont très compliquées. Trop compliquées, en tout cas, pour que la notion de mesure s'y applique. A et B peuvent bien être mesurables, les Ai et les Bi ne le sont pas (dans le cas général).
D'ailleurs, toute notion de mesure est totalement étrangère à la démonstration du théorème. Celle-ci repose plutôt sur des notions de théorie des ensembles (cardinaux, ensembles dénombrables) et d'algèbre pure : structure de groupe, action de groupe, ensemble dédoublable ; que l'on applique ensuite au groupe des isométries de l'espace.
Cela dit, l'existence du paradoxe apporte des informations utiles pour la théorie de la mesure (impossibilité d'une mesure universelle dans R3 -- il ne pourrait y avoir, par exemple, de paradoxe de H.-B.-T. sous une forme aussi générale dans le plan).