I. Algorithme de Horner
Il s'agit de calculer la valeur en un point d'un polynôme en ne faisant
que
des additions et des multiplications, grâce à l'écriture de
![P = a[p]*X^p+a[p-1]*X^(p-1)](graphics/module_polynomes1.gif) +...+
+...+
![]() sous la forme :
sous la forme :
P
= (( ... (
![]() )
)
![]() )
X
+ ... +
)
X
+ ... +
![]() )
)
![]()
Bien sûr,
Maple
sait calculer sur les polynômes, mais on n'utilisera pas cette possibilité dans cet exercice. On représentera un polynôme par la succession de ses coefficients
![]() , ...,
, ...,
![]() ,
,
![]() si
si
![P = a[p]*X^p+a[p-1]*X^(p-1)](graphics/module_polynomes10.gif) + ... +
+ ... +
![]() .
.
On va écrire une procédure
horner
prenant comme arguments
![]() , ...,
, ...,
![]() ,
,
![]() et retournant
P
(X). Donc : le nombre d'arguments de
horner
va être variable ; on aura à utiliser
args
et
nargs
(
aide
), et l'en-tête de la procédure sera de la forme
horner:=proc()
. Attention,
et retournant
P
(X). Donc : le nombre d'arguments de
horner
va être variable ; on aura à utiliser
args
et
nargs
(
aide
), et l'en-tête de la procédure sera de la forme
horner:=proc()
. Attention,
![]() va être le
va être le
![]() argument ("
args[1]
"), car c'est par lui que le calcul commence.
argument ("
args[1]
"), car c'est par lui que le calcul commence.
1.
Version itérative
. Ecrire la procédure
horner
en effectuant les additions et les multiplications à l'aide d'une boucle
for
. On pourra gérer une variable
P
dans la procédure, qui commencera par valoir 0 puis
![]() , puis
, puis
![]() , puis
, puis
![]() et ainsi de suite.
et ainsi de suite.
| > |
2. Version récursive . Pour éviter d'avoir à utiliser une variable, écrire une procédure horner2 sous forme récursive (s'appelant elle-même).
| > |
3.
Tester les deux procédures ci-dessus en calculant p. ex. le polynôme
 , ce qui doit répondre à la formule
horner(1,2,3)
(
resp
.
horner2(1,2,3)
).
, ce qui doit répondre à la formule
horner(1,2,3)
(
resp
.
horner2(1,2,3)
).
| > |
| > |
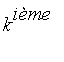 polynôme interpolateur élémentaire de Lagrange associé aux réels
polynôme interpolateur élémentaire de Lagrange associé aux réels
 = Product((X-x[j])/(x[k]-x[j]),j)](graphics/module_polynomes24.gif) ,
,
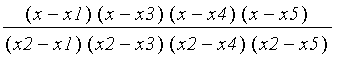 .
.
![P(x) = Sum(b[k]*L[k](x),k = 1 .. n)](graphics/module_polynomes39.gif) .
.
 ,
,