1. Calcul de la distance à un s.e.v.
On se propose de retrouver le calcul, fait en exercice, de la quantité suivante :
^2,x = 0 .. 1))](graphics/module_bilineaire1.gif)
Définir le produit scalaire approprié à ce calcul.
Définir les fonctions
f
:
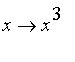 et
et
![g = g[a,b,c]](graphics/module_bilineaire3.gif) :
:
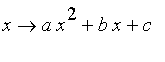 .
.
Écrire les trois conditions caractérisant le projeté orthogonal de la fonction
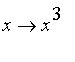 sur l'espace des fonctions polynomiales de degré
sur l'espace des fonctions polynomiales de degré
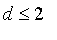 . On placera ces trois équations dans un
ensemble
.
. On placera ces trois équations dans un
ensemble
.
Résoudre le système formé par les trois conditions précédentes et affecter dans
a
,
b
et
c
les valeurs correspondantes (
assign
).
a
,
b
et
c
contenant maintenant les bonnes valeurs, faire effectuer par
Maple
le calcul approprié à la détermination de
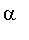 .
.
2. Étude de matrice orthogonale
Définir la matrice
A
suivante, qui représente l'endomorphisme
f
de
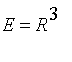 dans la base canonique (utiliser
array
ou
matrix
) :
dans la base canonique (utiliser
array
ou
matrix
) :
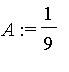 .
.
![matrix([[-8, -1, -4], [4, -4, -7], [-1, -8, 4]])](graphics/module_bilineaire10.gif)
En multipliant
A
par sa transposée, vérifier que
A
est bien une matrice orthogonale. Ne pas oublier
evalm
et
&*
.
Calculer
 et en déduire la nature géométrique de
f.
et en déduire la nature géométrique de
f.
Calculer la trace de
A
et en déduire la valeur de "
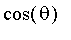 " (notation du cours).
" (notation du cours).
Définir la matrice identité
![I[3]](graphics/module_bilineaire13.gif) (penser à l'option
identity
de
array
). Utiliser l'instruction
linsolve
(
aide
) pour trouver l'axe de la rotation
f.
(penser à l'option
identity
de
array
). Utiliser l'instruction
linsolve
(
aide
) pour trouver l'axe de la rotation
f.
L'ensemble des solutions prend la forme d'un triplet dépendant d'un paramètre
_t1
-- c'est une variable utilisée par
Maple
. Donner à celle-ci une valeur quelconque afin d'obtenir un vecteur directeur
![a[1]](graphics/module_bilineaire14.gif) de l'axe de
f.
de l'axe de
f.
Attention,
![a[1]](graphics/module_bilineaire15.gif) est un vecteur. Pour le réutiliser (le multiplier par un scalaire, puis l'inclure dans une matrice de passage) il faut le transformer en liste (
convert(...,list)
) et le développer (
expand
), de telle sorte que le coefficient scalaire soit distribué.
est un vecteur. Pour le réutiliser (le multiplier par un scalaire, puis l'inclure dans une matrice de passage) il faut le transformer en liste (
convert(...,list)
) et le développer (
expand
), de telle sorte que le coefficient scalaire soit distribué.
Normer
![a[1]](graphics/module_bilineaire16.gif) , et effectuer les manipulations ci-dessus en appelant
a
le résultat.
, et effectuer les manipulations ci-dessus en appelant
a
le résultat.
Choisir n'importe quel vecteur
![b[1]](graphics/module_bilineaire17.gif) orthogonal à
a
et effectuer les même opérations que pour
orthogonal à
a
et effectuer les même opérations que pour
![a[1]](graphics/module_bilineaire18.gif) .
.
Faire calculer par Maple le vecteur
c
tel que (
a
,
b
,
c
) soit une BON de
E
. Normer et développer
c
comme
a
et
b.
À l'aide éventuellement d'un schéma, retrouver une expression de "
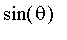 " et la faire calculer par
Maple
.
" et la faire calculer par
Maple
.
À titre de vérification, définir la matrice de passage
P
de la base canonique à (
a
,
b
,
c
), c'est à dire la matrice dont les
colonnes
(attention !) sont les vecteurs
a
,
b
et
c.
Utiliser alors cette matrice pour déterminer la forme "simple" d'une matrice semblable à
A
et retrouver ainsi les valeurs calculées de
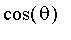 et
et
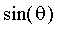 .
.
^2,x = 0 .. 1))](graphics/module_bilineaire1.gif)
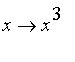 et
et
![]() :
:
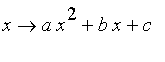 .
.
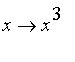 sur l'espace des fonctions polynomiales de degré
sur l'espace des fonctions polynomiales de degré
![]() . On placera ces trois équations dans un
ensemble
.
. On placera ces trois équations dans un
ensemble
.
![]() .
.
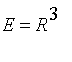 dans la base canonique (utiliser
array
ou
matrix
) :
dans la base canonique (utiliser
array
ou
matrix
) :
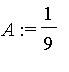 .
.
![matrix([[-8, -1, -4], [4, -4, -7], [-1, -8, 4]])](graphics/module_bilineaire10.gif)